Fibonacci Strategy

The Fibonacci Strategy is a popular method used in various fields such as trading, gambling, and even in personal development. Drawing inspiration from the Fibonacci sequence—a series of numbers where each number is the sum of the two preceding ones—this strategy aims to create a structured approach to decision-making that can maximize gains while minimizing risks. Through an exploration of its principles and applications, we will uncover the depths of the Fibonacci Strategy and how it may be integrated into your own practices.

Understanding the Fibonacci Sequence and Its Origins

To fully comprehend the Fibonacci Strategy, it’s essential to first understand https://f8bett.city/ the origins of the Fibonacci sequence itself. This sequence was introduced to the Western world by Leonardo of Pisa, more widely known as Fibonacci, in his 1202 book “Liber Abaci.” The sequence starts with the numbers 0 and 1, followed by the sum of the last two numbers: 0, 1, 1, 2, 3, 5, 8, 13, and so forth.

At its core, the Fibonacci sequence embodies the beauty of nature’s patterns, seen in everything from the arrangement of leaves on a stem to the spirals of seashells. This intrinsic connection to organic growth and natural phenomena has made the Fibonacci sequence a compelling subject of study not only in mathematics but also in art, architecture, and now, financial strategies.

The essence of the Fibonacci sequence translates beautifully into strategic applications. The inherent nature of the sequence offers a progressive structure that can guide individuals in making calculated decisions based on previous experiences. As we move forward, we will explore how this mathematical notion finds expression in various fields and ultimately leads us to the development of the Fibonacci Strategy.

Exploring the Mathematical Foundations

The Fibonacci sequence might appear simple at first glance, yet its application involves deeper mathematical principles that many find intriguing.

Mathematically, one can represent the Fibonacci sequence through a recursive formula:

• F(n) = F(n-1) + F(n-2)

This implies that each number in the sequence can be derived from the previous two. Beyond mere arithmetic, this sequence can lead to discussions about ratios, specifically the golden ratio (approximately 1.618), which appears when you divide consecutive Fibonacci numbers.

The remarkable aspect of the Fibonacci sequence is its omnipresence in the universe. For instance, flowers display petal arrangements that correspond to Fibonacci numbers, and galaxies spiral in accordance with these principles. This universality lends credence to theories suggesting that the Fibonacci sequence—and consequently, the Fibonacci Strategy—holds not just numerical significance but philosophical depth as well.

Connections to Nature

As previously mentioned, the Fibonacci sequence finds manifestation in numerous natural phenomena. This raises an important question: What does this indicate about human behavior and decision-making?

In looking toward nature for insights, we begin to see how the Fibonacci Strategy can help individuals align their actions with innate patterns found within the world. For instance, the way trees branch out often follows Fibonacci principles. This branching pattern ensures optimal sunlight exposure and nutrient absorption, showcasing efficiency in growth and survival—qualities that anyone can apply to their personal or professional endeavors.

By recognizing these patterns in nature, the application of the Fibonacci Strategy becomes clearer. It encourages individuals to consider the steps they take in their journey rather than rushing to achieve instant results. Just like a tree takes its time to grow, one must embrace the iterative process of learning and adapting.

The Role of Ratios and Proportions

Another mathematical aspect worth mentioning is the role of ratios in the Fibonacci sequence. The ratio between successive Fibonacci numbers converges on the golden ratio as the numbers increase. This ratio not only possesses aesthetic appeal in design and art but also serves as a guiding principle in resource allocation decisions within the Fibonacci Strategy.

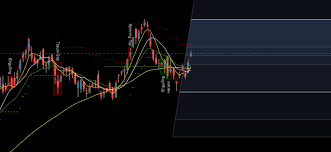
In finance and trading, traders have developed tools such as Fibonacci retracement levels. These levels are derived from the sequence and are utilized to identify potential support and resistance levels during market movements. By mapping out these levels, traders can improve their risk management strategies, allowing them to enter and exit positions more effectively. This mathematical understanding transforms abstract numbers into actionable insights, providing a clear roadmap for decision-making.